13-understanding-bayes

简介

下面我们考察一下一枚硬币真实参数为:p(head)=0.6的硬币在不同观察结果(obs)下的似然率估计

估计两个点p(head)=[a=0.5,b=0.8]

在这两个点的最大似然率的估计可以表示为赔率(odds), 注意这不是概率

可以直观的在概率密度图上观察到两者的差异

当 观测值逐渐增加以后, 两个点的条件概率会趋近于 0, 赔率会趋近于 1 \[L(a,b)=\frac{p(obs|a)}{p(obs|b)}\]

1. load package

 using Distributions,GLMakie

2. define likelihood function

xc=[0.5,0.8]
function plot_likelihood(;p=0.6,n=10,s=6)
    probrange=range(0.0,1.0,50)
    fig=Figure(resolution=(500,300))
    ax=Axis(fig[1,1])
    fun(p)=Binomial(n,p)|>d->pdf(d,s)
    data=Float64[fun(p) for p in probrange]
    

    pdf1=fun(xc[1]);pdf2=fun(xc[2])
    lines!(ax,probrange,data,label="n=$(n),success=$(s)")
    scatter!(ax,xc,[pdf1,pdf2];color=[:red,:green],markersize=20)
    lines!(ax,[xc[1],xc[2],xc[2]],[pdf1,pdf1,pdf2];linestyle=:dot)
    axislegend(halign =:left, valign =:top)
    fig
end

plot_likelihood (generic function with 1 method)

---

3. plot results

3.1 10 次硬币试验,6 次正面

两个点的高度相除就是基于实验观察的赔率

plot_likelihood()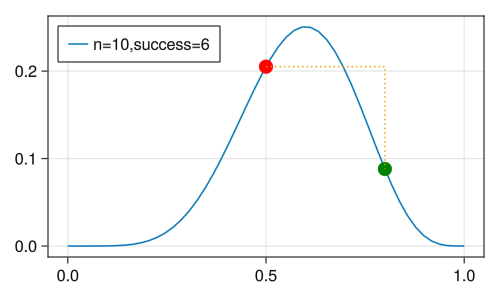

3.2 100次试验 60 次正面

plot_likelihood(;p=0.6,n=100,s=60)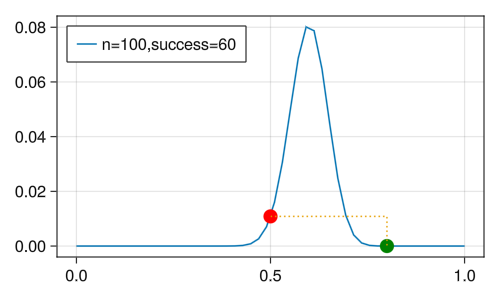

3.3 500次试验,300 次正面

plot_likelihood(;p=0.6,n=500,s=300)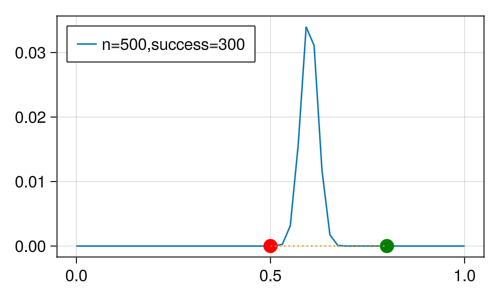

在上述实验中模型参数是事先知道的:p(head)=0.6,但是对于很多问题, 参数未知. 在这种情况下, 如果给定两个参数, 优先选择赔率最大的参数作为估计