4-single-variable-integral

一元函数积分示意

欧拉方法, 改变Δx, 提高近似精度

使用 rect = Rect(start-x,start-y,width,height)方法 绘制线性近似的矩形

• start-x: 初始的点的 x 坐标
• start-y 初始的点的 y 坐标 这里为 0 矩形初始点都在 x轴上
• width Δx
• height 函数值

fig[fldmod1(idx,3)...] fldmod1 方法来生成 plot layout

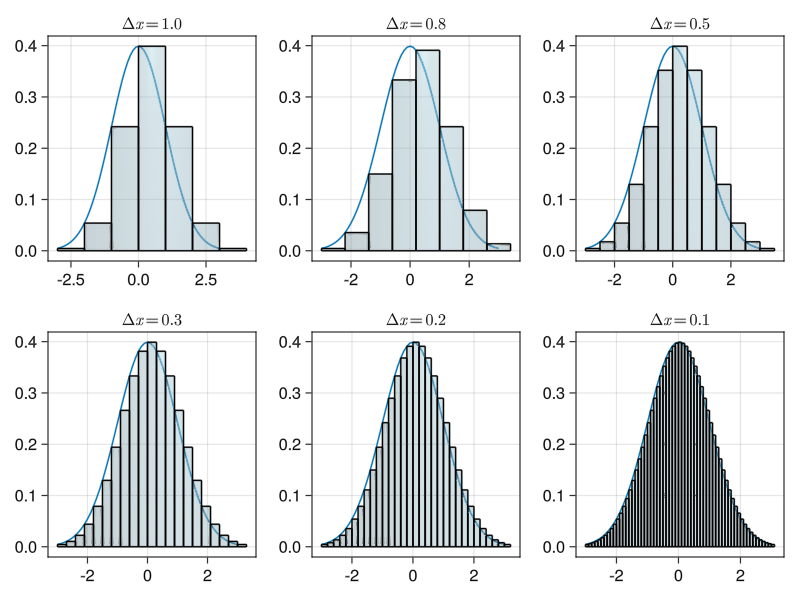
using GLMakie,Distributions,Pipe

ws=[1,0.8,0.5,0.3,0.2,0.1] #Δx 数组
d=Normal()
xs=-3:0.1:3 
ys=pdf.(d,xs)

"""
## define Rect
rect = Rect(start-x,start-y,width,height)
"""
function  rect(;x=0,w=0.5)
    return  Rect(x,0,w,pdf.(d,x))
end


function plot_hist(ax,box)
    mesh!(ax, box, color=(:lightblue,0.4))
    wireframe!(ax, box; color = :black, transparency=true)
end

function plot_res()
    fig=Figure()
    for (idx,w) in enumerate(ws)
        local ax=Axis(fig[fldmod1(idx,3)...],title=L"Δx=%$(w)")
        lines!(ax,xs,ys)
        @pipe  Vector(-3:w:3).|>rect(;x=_,w=w).|>plot_hist(ax,_)
    end
    fig
    #save("one-single-variable-euler-method-2.png",fig)
end

plot_res()