7-what is dimension in mathematics?

info

ref: Understanding Regression Analysis ch06 figure 6.3

What is a dimension? This is a very difficult problem to understand. The most basic problem in mathematics is the measurement of the physical properties of reality. The most commonly used tool for measuring is a ruler. We can turn the dimension problem into another problem, and to measure the differences between different objects in a set, we need several rulers that cannot replace each other

什么是维度.这是一个非常难理解的问题.数学最基础的问题是对现实实物属性的度量.度量最常用的工具是直尺. 我们可以把维度问题转化为另一个问题,要度量一个集合中不同对象的差异 ,需要几把不能相互代替的尺子

using CairoMakie,Distributions,Turing,LinearAlgebra
using Plots,StatsPlots
import CairoMakie:wireframe!,scatter!

1 生活在三维空间中平面的维度

xs=ys=Vector(1:0.05:2)
zs1=[-1+6*x+10*y for x in xs ,y in ys]
zs2=[0 for x in xs, y in ys]

21×21 Matrix{Int64}:
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0

function plot_wireframe(zs::Matrix)
    fig=Figure()
    ax=Axis3(fig[1,1],azimuth=-pi/4)
    wireframe!(ax,xs,ys,zs)
    fig
end

function plot_wireframe(zs1::Matrix,zs2::Matrix)
    fig=Figure()
    ax=Axis3(fig[1,1],azimuth=-pi/4)
    wireframe!(ax,xs,ys,zs1,color=:green)
    wireframe!(ax,xs,ys,zs2,color=:red)
    
    fig
end

plot_wireframe (generic function with 2 methods)

plot_wireframe(zs1)

Figure 1: plane-in-3d-space

plot_wireframe(zs1,zs2)

Figure 2: plane-and-projection-in 2d plane

Figure 2 中 度量两个平面的工具是一样. 我们只考虑平面中点之间的属性的差异,脱离三维空间. 绿色平面和红色平面度量方法相同, 只需要两种不同的尺子,度量 x,y 方向的属性就可以分开平面里的不同个体.

2. add some noise

在上面图的基础上,我们可以增加一些噪音

d=Normal(0,2)
zs4=[[x,y,-1+6*x+10*y+rand(d)] for x in xs  for y in ys]
matrix=hcat(zs4...)

3×441 Matrix{Float64}:
  1.0      1.0      1.0      1.0     …   2.0      2.0      2.0      2.0
  1.0      1.05     1.1      1.15        1.85     1.9      1.95     2.0
 15.4722  17.5936  15.6399  17.2154     26.8933  29.1061  29.4819  33.3816

这时,两个尺子就不够了. 还需要度量噪音,这就是第三位维度

with different noise

σs=[0.0,0.05,0.1,1,1.5,3]
dists=[Normal(0,σ) for σ in σs ]

6-element Vector{Normal{Float64}}:
 Normal{Float64}(μ=0.0, σ=0.0)
 Normal{Float64}(μ=0.0, σ=0.05)
 Normal{Float64}(μ=0.0, σ=0.1)
 Normal{Float64}(μ=0.0, σ=1.0)
 Normal{Float64}(μ=0.0, σ=1.5)
 Normal{Float64}(μ=0.0, σ=3.0)

在不同噪音情况下的平面变化情况

function plot_matrix_arr()
    fig=Figure(resolution=(1200,800))
    
     for  idx in eachindex(dists)
          zs=[[x,y,-1+6*x+10*y+rand(dists[idx])] for x in xs  for y in ys]
          matrix=hcat(zs...)
          ax=Axis3(fig[fldmod1(idx,3)...],title="σ=$(σs[idx])",azimuth=pi/8,elevation=-pi/4)
          scatter!(ax,matrix,color=(:blue,0.5),strokewidth=0.5, strokecolor=:black)
     end
     fig
end
plot_matrix_arr()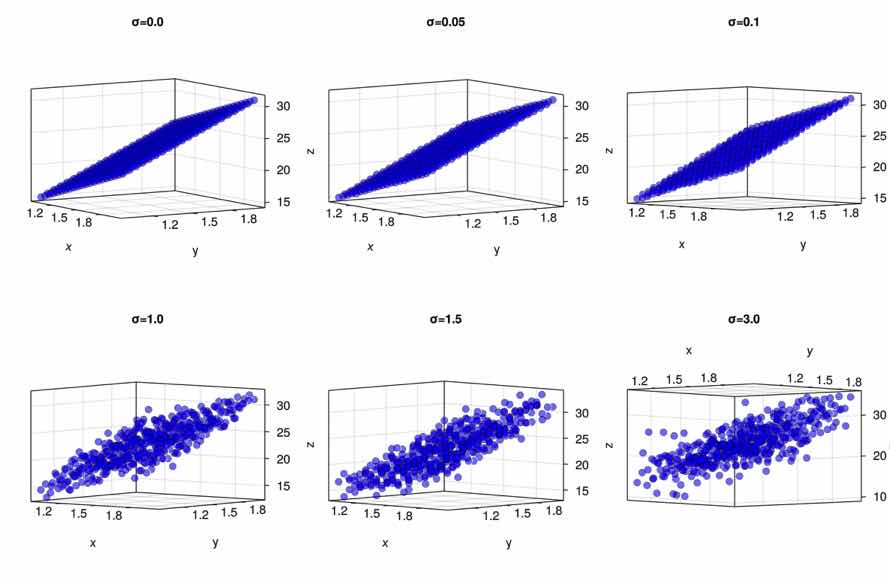

rotation

3. Bayesian Infrence

在上面的的图示中, 我们通过添加噪音获得了数据, 通过添加正态分布的噪音,使得数据 形成三个维度, 第三个维度是不确定性因素, 因此可以通过贝叶斯方法推断不确定因素

3.1 生成数据

d=Normal(0,3)
zs=[-1+6*x+10*y+rand(d) for x in xs  for y in ys]
X=hcat(xs,ys)

21×2 Matrix{Float64}:
 1.0   1.0
 1.05  1.05
 1.1   1.1
 1.15  1.15
 1.2   1.2
 1.25  1.25
 1.3   1.3
 1.35  1.35
 1.4   1.4
 1.45  1.45
 1.5   1.5
 1.55  1.55
 1.6   1.6
 1.65  1.65
 1.7   1.7
 1.75  1.75
 1.8   1.8
 1.85  1.85
 1.9   1.9
 1.95  1.95
 2.0   2.0

3.2 Turing workflow

@model  function linear_regression(X,y)
       n = length(y)
       mu=[-1+6*x+10*y  for x in X[:,1]  for y in X[:,2]]
       σ² ~ truncated(Normal(0, 5); lower=0)
       for i in 1:n
       y[i] ~ Normal(mu[i], σ²)
       
    end
end

linear_regression (generic function with 2 methods)

3.3 random sampling

model = linear_regression(X,zs)
chain = sample(model, NUTS(), 5_000)

┌ Info: Found initial step size
└   ϵ = 0.00625
Sampling:  20%|████████▎                                |  ETA: 0:00:00Sampling: 100%|█████████████████████████████████████████| Time: 0:00:00

Chains MCMC chain (5000×13×1 Array{Float64, 3}):
Iterations        = 1001:1:6000
Number of chains  = 1
Samples per chain = 5000
Wall duration     = 7.53 seconds
Compute duration  = 7.53 seconds
parameters        = σ²
internals         = lp, n_steps, is_accept, acceptance_rate, log_density, hamiltonian_energy, hamiltonian_energy_error, max_hamiltonian_energy_error, tree_depth, numerical_error, step_size, nom_step_size
Summary Statistics
  parameters      mean       std   naive_se      mcse         ess      rhat    ⋯
      Symbol   Float64   Float64    Float64   Float64     Float64   Float64    ⋯
          σ²    2.8191    0.0944     0.0013    0.0019   2258.7134    1.0000    ⋯
                                                                1 column omitted
Quantiles
  parameters      2.5%     25.0%     50.0%     75.0%     97.5% 
      Symbol   Float64   Float64   Float64   Float64   Float64 
          σ²    2.6411    2.7545    2.8171    2.8807    3.0125

Plots.plot(chain)

3.4 bayesian Workflow

下面总结一下流程,在贝叶斯统计中,对于使用软件包的人来讲, 理解采样过程 不是必须的,但是需要理解采样过程在流程中处于什么位置. 使用软件包要关注如何 使用概率分布构建模型, 贝叶斯采样时如何起作用的

flowchart TD 
  Init("building model")
  
  A["Normal(μ=0,σ=0.05)"] 
  B["Normal(μ=0,σ=0.1)"] 
  C["Normal(μ=0,σ=0.5)"] 
  D["Normal(μ=0,σ=1.5)"] 
  E["Normal(μ=0,σ=2)"] 
  F["Normal(μ=0,σ=3)"] 
  G[(Data)]
  Init-->A
  Init-->B 
  Init-->C
  Init-->D
  Init-->E
  Init-->F
  A-->G
  B-->G 
  C-->G 
  D-->G
  E-->G 
  F-->G

Figure 3: bayesian-workflow

在 Figure 3 中 我们可以设定一系列不同参数的 概率分布, 然后从每个模型中随机采样, 计算最大似然率.

遍历概率模型的参数生成不同的概率分布, 然后从中采样, 生成数据与 观测数据最为相似的参数就作为模型的最优参数.

抽样方法影响参数精度, 但是不改变工作流程.