12-likelihood of coin toss

Author

math4mad

简介

likelihook解释参见:understanding-bayes-a-look-at-the-likelihood

硬币试验似然率的流程

问题:硬币的\(p(head)=?\)
模型:二项式分布
搜索所有\(p(head)\) 产生观测结果的概率, 选出最有可能的一个 \(p(head)\)

似然率要解决的问题对于投掷 10 次硬币, 获取 7 次正面的结果 pdf(Binomial(10,0.5),data=7)

pdf(Binomial(10,0.7),data=7)

pdf(Binomial(10,0.1),data=7)

返回值都不为 0,意思是p(head)=[0.1,0.5,0.7]的硬币都有机会获得这个观测结果在这种硬币P(head)参数未知的情况下, 我们挑选出最有可能的一个参数值,这就是最大似然率估计

1. load package

Code

using Distributions,GLMakie,Random,Pipe
Random.seed!(123)

TaskLocalRNG()

2. 基本概率模型:二项式分布

Code

@doc(Binomial)

Binomial(n,p)

A Binomial distribution characterizes the number of successes in a sequence of independent trials. It has two parameters: n, the number of trials, and p, the probability of success in an individual trial, with the distribution:

\[ P(X = k) = {n \choose k}p^k(1-p)^{n-k}, \quad \text{ for } k = 0,1,2, \ldots, n. \]

Binomial()      # Binomial distribution with n = 1 and p = 0.5
Binomial(n)     # Binomial distribution for n trials with success rate p = 0.5
Binomial(n, p)  # Binomial distribution for n trials with success rate p

params(d)       # Get the parameters, i.e. (n, p)
ntrials(d)      # Get the number of trials, i.e. n
succprob(d)     # Get the success rate, i.e. p
failprob(d)     # Get the failure rate, i.e. 1 - p

External links:

Binomial distribution on Wikipedia

3. 硬币试验的不同观测值概率模型定义

定义input_data 函数接受data观测值,返回一个新的函数, 参数是概率值, 返回值为概率密度

Code

@kwdef struct CoinToss
    total::Int=10
    success::Int=7
end
function input_data(params::CoinToss)
   total,success=params.total,params.success
   return  (p::Real)-> @pipe Binomial(total,p)|>pdf(_,success)
end

input_data (generic function with 1 method)

4. 10次试验,不同正面观察结果下的概率密度图

Code

probrange=range(0.0,1.0,50)
success_arr=0:10  #不同正面次数
fig=Figure(resolution=(600,600))
for i in success_arr
    params=CoinToss(success=i)
    local row= div(i,3)
    local col=rem(i,3)
    local ax=Axis(fig[row+1,col])
    
    local likelihood=input_data(params)
    max_likelihood=likelihood.(probrange)|>maximum
    x=undef
    for i in probrange
        if likelihood(i)==max_likelihood
            x=round(i,digits=2)
           
        end
    end
    lines!(ax,probrange,likelihood.(probrange),label="head=$(i)")
    vlines!(ax,[x],label="p=$(x)")
    ax.title="head=$(i),p=$(x)"
   
end
fig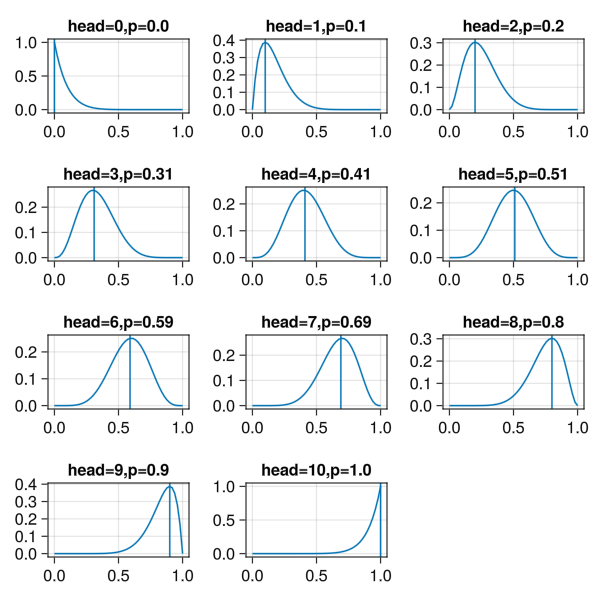

5. 最大似然率估计的正式方法

Distributions.jl提供了fit_mle函数

Code

@doc(fit_mle)

fit_mle(D, x)

Fit a distribution of type D to a given data set x.

For univariate distribution, x can be an array of arbitrary size.
For multivariate distribution, x should be a matrix, where each column is a sample.

fit_mle(D, x, w)

Fit a distribution of type D to a weighted data set x, with weights given by w.

Here, w should be an array with length n, where n is the number of samples contained in x.

fit_mle(::Type{<:Beta}, x::AbstractArray{T})

Maximum Likelihood Estimate of Beta Distribution via Newton’s Method

fit_mle(::Type{<:Weibull}, x::AbstractArray{<:Real}; 
alpha0::Real = 1, maxiter::Int = 1000, tol::Real = 1e-16)

Compute the maximum likelihood estimate of the Weibull distribution with Newton’s method.

Code

for i in 1:10
@info "total=10,success=$i mle"=> fit_mle(Binomial, 10,[i])
end

[ Info: "total=10,success=1 mle" => Binomial{Float64}(n=10, p=0.1)
[ Info: "total=10,success=2 mle" => Binomial{Float64}(n=10, p=0.2)
[ Info: "total=10,success=3 mle" => Binomial{Float64}(n=10, p=0.3)
[ Info: "total=10,success=4 mle" => Binomial{Float64}(n=10, p=0.4)
[ Info: "total=10,success=5 mle" => Binomial{Float64}(n=10, p=0.5)
[ Info: "total=10,success=6 mle" => Binomial{Float64}(n=10, p=0.6)
[ Info: "total=10,success=7 mle" => Binomial{Float64}(n=10, p=0.7)
[ Info: "total=10,success=8 mle" => Binomial{Float64}(n=10, p=0.8)
[ Info: "total=10,success=9 mle" => Binomial{Float64}(n=10, p=0.9)
[ Info: "total=10,success=10 mle" => Binomial{Float64}(n=10, p=1.0)